Day 29 of #100daysofnetworks
Paper: Mining Bursting Communities in Temporal Graphs + Original Implementation
Hi everybody. Over the last three days, I’ve written about how to identify dense communities in networks. While investigating some of these communities, I ran into a paper with an interesting title.
Today’s post has two parts. I describe the paper, and I show my own personal implementation I came up with on the spot, to experiment with the idea of the paper.
Let me break this down a bit.
Mining: identifying and extracting useful context
Bursting Communities: communities pop in and out of existence
Temporal Graphs: network graphs of a period of time
Putting this together, the authors are attempting to identify and extract useful context about communities that pop into existence at a moment or period in time. Why would that happen?
In their paper, they discuss a few reasons why this might happen:
Human communication events occur in a short time
A bursty pattern can show multiple events happening at the same time
These events could represent emerging activity or behavior
This can help detect emergency events, that something went very bad
But emergent behavior can also show something very good happening. Maybe a new idea has been created and suddenly everyone is writing research papers on the subject. Or maybe a free concert is happening at the park.
I recommend reading their paper, as they have an interesting solution using a mix of software engineering and multiple different methods of detection.
I was going to read the paper and call it a day, but that’s not how my mind works, so I thought I’d use some of my previous work to show some of these bursting communities.
But before I move on, the paper did accidentally highlight something: Network Science researchers are still using stale well-known datasets to identify phenomenon, which makes sense in some cases. However, this phenomenon can easily be shown with any of the #100daysofnetworks datasets that contain date fields. With that, you can create a temporal graph. With a temporal graph, you will almost certainly run into some kind of bursting behavior. You should study using interesting data that you are curios about, not just what is on hand, if you can. I show you how.
So, for today’s example, I’m using yesterday’s Artificial Life arXiv dataset that I compiled. That’s much more interesting than an Enron dataset from 1999, in my opinion.
Show and Tell Time!
First, get the code and follow along. You will want to pay attention and go very slow if you are new to networks. If you are new, think more about the possibilities, and revisit earlier days in this series. This is very advanced. I am pushing my own abilities with this one.
After loading the Artificial Life dataset, I do things a little differently than before. I use a Python dictionary for G to store each “time slice”, as I call them. I then took the enrichment function from Day 13 and made some useful modifications and additions.
With the enrichment, each time slice looks something like this:
{'graph': <networkx.classes.graph.Graph at 0x25279d5c5c8>, 'dropped_edges': [('Junji Suzuki', 'Kunihiko Kaneko'), ('S. T. Petcov', 'A. Yu. Smirnov')], 'added_edges': [('B. B. Levchenko', 'C. Riccardi'), ('B. B. Levchenko', 'G. Boca'), ... lots more ... ('V. Arena', 'V. A. Nechitailo')], 'dropped_nodes': ['A. Yu. Smirnov', 'Junji Suzuki', 'Kunihiko Kaneko', 'S. T. Petcov'], 'dropped_node_count': 4, 'added_nodes': ['B. B. Levchenko', ... lots more ... 'V. Arena'], 'added_node_count': 13, 'graph_dropped': <networkx.classes.graph.Graph at 0x25203b0e788>, 'graph_added': <networkx.classes.graph.Graph at 0x25203b0ecc8>, 'density_change': 0.6666666666666667, 'degree_change': 9, 'edge_change': 76, 'graph_core': <networkx.classes.graph.Graph at 0x25203b28348>, 'graph_core_node_count': 13, 'graph_core_edge_count': 78}
That is ONE time slice. There are many. This little window in time shows that there have been various changes in the network. I love this little enrichment function that has come from this series. It is so useful.
And with that, each time slice can be mined for bursting communities.
I didn’t want to copy the paper. Their techniques are interesting, but so are mine.
Approach 1: Added Node Counts
This idea is simple enough. If suddenly, in a moment of time, 1000 people show up in one place, that might be worth looking into. However, that doesn’t always show an emergency. For instance, in this dataset, the Artificial Intelligence ecosystem is always noisy. To find bursts, I have to set a high threshold, to look for unusual bursts of activity. You can see the code to understand how I played with this idea.
This identified a big burst of activity at a given time.
And since I captured the core during the enrichment step, I can look at that too.
Ok, cool. this tells me something. A big group of people wrote a paper and everyone put their name on it. That’s definitely a burst, but is it unusual? That’s a question for another day. That’s a question about understanding the ecosystem itself, which is a higher level question, and kind of intriguing.
Approach 2: K_core Node Counts
This one is a bit inspired by the paper. To do this, I captured the core of each network time slice, and then counted the nodes in the core. Check my code for implementation details.
With a little code, we can identify when large clusters show up in a network.
threshold = 50
result_df = result_df[result_df['graph_core_node_count']>threshold]
title = 'Graph Core Node Count by YEARMONTH'
_= result_df['graph_core_node_count'].plot.bar(figsize=(16, 8), title=title)
These are the results. I’ve filtered to time slices that have 50 or more nodes in the core at each given moment of time. Each of these can also be investigated and explored.
Approach 3: Density Increase
There are so many ways this idea can be approached. After reading this, after getting to known networks a bit better, think about how you would approach this. How would you identify bursts of activity in a complex network, using graph data?
I used a very simple approach, just for this exercise. This is not finished code. This is a first attempt.
threshold = .1
result_df = result_df[result_df['density_change']>threshold]
title = 'Density Change by YEARMONTH'
_= result_df['density_change'].plot.bar(figsize=(16, 8), title=title)
This is actually very interesting. Look all the way to the right. What do you notice? WHAT IN THE WORLD? Why is there nothing after February 2014? Is this a bug? I started getting nervous when I saw that. So, I looked closer. These are all the months where network density increased by more than 0.1. Did I accidentally leave in a filter while debugging? What did I do wrong?
202204 -0.00183 202205 0.034756 202206 -0.034125 202207 -0.000088 202208 -0.002865 202209 0.007511 202210 -0.001453 202211 -0.007569 202212 0.00016 202301 0.000163 202302 0.001126 202303 0.005355 202304 -0.006539 202305 -0.001437 202306 0.004352 202307 -0.001395 202308 0.01193 202309 -0.012969 202310 -0.001433
Nothing. It turns out that the Artificial Intelligence and Artificial Life ecosystem is so dense that network density increases and decreases by a little bit every month.
So, everything above a 0.1 threshold actually was a significant burst. The network became denser during those times than more recent times. That’s a cool insight! What does it mean?! Has anybody studied this or written about this phenomenon? Cool!
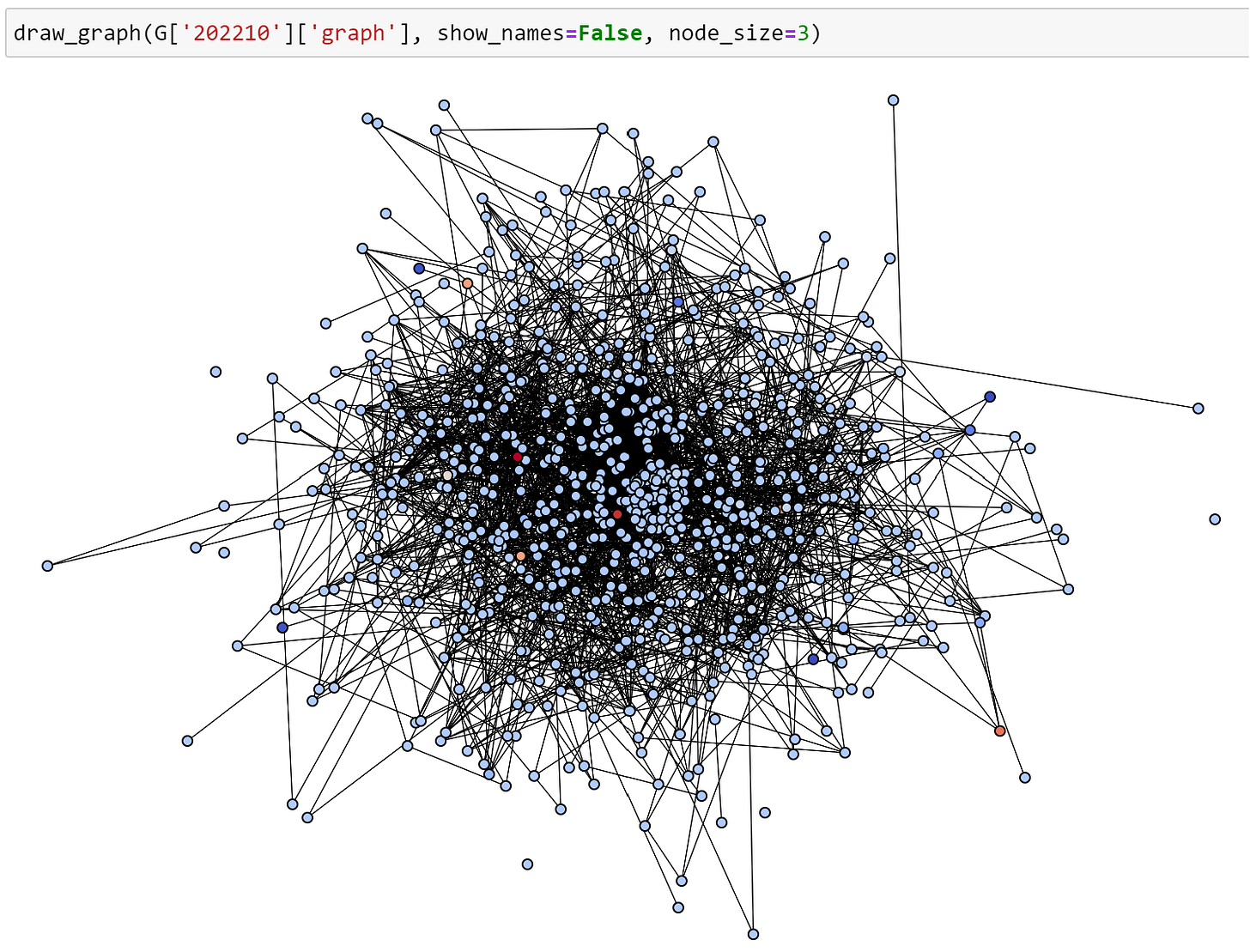
When investigating one of these bursts, I saw this. Notice the two dense circles. Those have increased the overall density of the graph at that moment in time. Two papers were written with many authors involved, and they know each other. If those two papers hadn’t been written, density would be very low. Hey, that’s a burst!
So, this approach will even work when networks are just starting to develop, because initially, there are often large changes to density. Three people who known each other will appear as a subgraph with 1.0 density, for instance.
A Few More Thoughts
This is a really cool paper. Research papers give possible approaches, not a dogmatic set of rules. I was inspired by their paper and used that I had previously built and was able to identify bursting communities in only a few hours. Work builds on work builds on work builds on work. The biggest contribution today came from Day 13, as it took very little to take inspiration from their idea and implement it in my code. The enrichment function now has some new context to explore!
I also really liked the idea of “Average Separability (AS)”, though I would give it a different name. The way I understand it, it is essentially:
AS = Community Density / Overall Density
I think that’ll be a fun idea to explore on another day. That seems useful, to me.
The authors also mention something called DENSEST that I’d like to take a look at and see if it can be useful, more useful than my own approaches.
Alright, that’s enough. I was going to just read a research paper and relax, but I couldn’t resist doing all of this. When I get inspired, there’s no breaks.
That’s All, Folks!
That’s all for today! Thanks for reading! If you would like to learn more about networks and network analysis, please buy a copy of my book!