Hi everybody. Happy weekend. One of my favorite things to do with networks is to use them to simulate some phenomenon I have noticed in the real world. The ability to explore and understand the world around me is one of the main attractions of network science and social network analysis to me. Natural Language Processing (NLP) and Network Science together make these possible, and I try to communicate that with this series, encouraging others to explore their own existence.
Last week, I used GPT 4.0 to make this image to supplement the article:
I like this image for a few reasons:
It looks like me when I was younger, only better dressed. AI gave it the right number of fingers, so that’s a plus. The image captures my curiosity and intensity.
I made this image to communicate the overlap between Network Science and Geospatial Analysis, but this also communicates that graphs are useful for exploring the real world and our own existence.
Geospatial allows us to explore the physical world, NLP gives us the ability to explore language use (how humans communicate), and Network Analysis allows us to explore how things relate to other things.
So, today, I made this image the official icon image for this blog series on Substack. I like this much better than the black and white image I previously had.
Noticing a Phenomenon
I’ve had an idea that has been rolling around in my head for a while, annoying me to the point that I needed to do something about it. This post is the result of this action.
Going back to the beginning, what is a node, and what is an edge? A node is any thing. Nodes can be people. Nodes can be animals. Nodes can be concepts. Nodes can be events. What is an edge? An edge is any relationship between two things. So, what is a network? A network is an object comprised of the relationships between things and other things.
So, let’s think about two different kinds of networks:
Social Networks are made of people and their relationships to other people
The internet is made of websites and their relationships to other websites
Are people all the same? Are websites all the same? Are animals all the same? Are dogs all the same? Are concepts all the same? Are words all the same?
The answer is a simple NO.
So, when we create a social network, we are creating a network of people and how they relate to other people. But are people all the same? Again, the answer is no. We need a way to understand the differences that are at play in the network.
Thinking about why people become friends, one reason is that they have something in common. There is a word for this: homogeneity.
Homogeneity: the quality or state of being all the same or all of the same kind.
Or, another way to put it: like attracts like. Think about who you are friends with? How much does your friend GROUP have in common? Do most people in the group have a lot in common, or is it a diverse group?
Like attracts like. People with one worldview will become friends with others who share the same worldview or have a compatible worldview. Those with an incompatible worldview, there is much less chance of a relationship forming.
Introducing Modularity
I have several books about networks and network analysis. One of my favorites “Networks” by Mark Newman.
Recently, while reading this book, I came across the concept of modularity.
Modularity is a measure of the extent to which like is connected to like in a network.
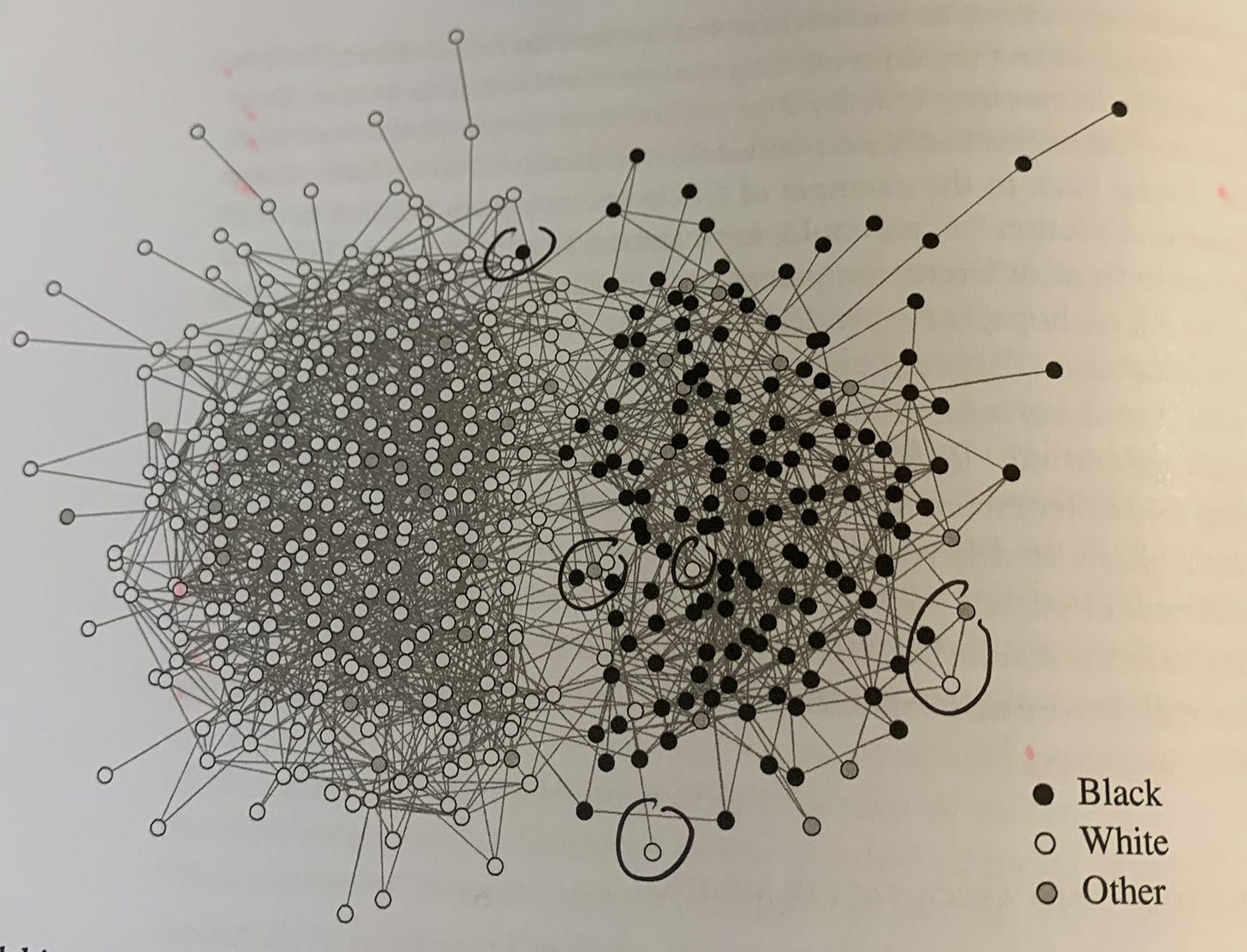
There is a Network Science measure of the extent that like attracts like in a network! Here is an illustration from the book.
When I saw this image, I was immediately inspired. This network shows how groups of different races interact with one another. I circled parts that were interesting to me, but there is some mixing taking place on the left side as well. It is just harder to see.
This is network of people. This image clearly demonstrates that people are not all the same. A network might be about one thing (people, websites, animals, concepts, words, etc), but those things have additional context that can be used as well.
Experiment: Simulating the Internet
In my work, I spend a lot of time analyzing the internet. The world wide web of today is comprised of billions of websites, in many different languages, with content about everything humans project onto the internet.
But with every network analysis I do, homogeneity is obvious in the communities I inspect. Like attracts like. But there is another hidden rule shown in the gaps: dislike repels dislike. And sometimes, dislike still gets a link (an angry hyperlink to complain about).
Today, I built a simulation to see what would happen if I applied some rules to how the network would form.
In the Jupyter notebook, I describe the experiment:
For this simulation, I am attempting to use rules of attraction to dictate how a network can form. I spend a lot of time analyzing the internet, and I want to see if I can simulate what I see in the wild.
On the internet, websites link to websites for a number of reasons, but they can be simplified down to two: homogeneity (like attracts like) and opportunity. Websites are created by people, and we network with other people for the same reasons. We form relationships with others who have similar world views as us, and we form relationships with others who may provide opportunities to us (even if we disagree with them).
This very rough simulation is just to see what happens when two things interplay: a) when rules determine connectivity, b) when there is very low probability of finding each other to make a connection.
First, I will set some worldviews. I'll just call them 0, 1, and 2. You could consider them leftwing, center, and rightwing. You could also consider them Klingon, Human, and Dog. I will specify a rule that both 0 and 2 can connect with 1, but 0 and 2 will not connect with one another. Their disagreement or misunderstanding is too deep.
I will also specify ten interests. I will later set a rule that interest 0 can link with all other interests, but no other interest linking can occur. If you think of these interests as internet categories, you could consider interest 0 as news, as lots of kinds of websites link to news (blogs, entertainment, social media, etc).
Of course, this is a simplistic experiment. Reality is much more complicated, but let's see what happens. Part of the power of doing network analysis programmatically is being able to set up creative simulations and see what happens.
These are the rules of connectivity:
worldview 1 can link to worldviews 0 and 2
worldviews 0 and 2 cannot link to each other
interest 0 can link to all other interests including 0
other interests can only link within the same interest
there is only a 10% chance of a connection being made, after the above rules are met
Today’s experiment is still incomplete, in progress. This is something new, and something I am going to spend some time on, because I have to think of a path forward in order to take this from theory to usefulness.
With these rules, a network does form.
And what is most interesting to me is that this is a network that was constructed using worldviews and interests, including a rule for incompatibility of world views. This makes sense to me, logically, much more than a random graph.
Zooming in on the ego graph, I can see that the nodes that are part of the small community have a range of worldviews and interests. This is the ego graph for the node with the highest Page Rank score.
At this level, we can’t see that these nodes are different. We can see that some are more important, by their node coloring, but we can’t see anything about the groups they belong to. I have to look at them differently, and I am still figuring out what I want to do. I could color the nodes by worldview, or I could color the nodes by interest. But I don’t need to decide that today. I can look at a text representation.
node: 101; worldview: 1; interests: [7] node: 188; worldview: 2; interests: [0, 6] node: 198; worldview: 1; interests: [2] node: 279; worldview: 1; interests: [2, 6] node: 307; worldview: 2; interests: [3, 1] node: 446; worldview: 0; interests: [9] node: 456; worldview: 2; interests: [0] node: 499; worldview: 0; interests: [0, 6] node: 505; worldview: 2; interests: [9] node: 508; worldview: 2; interests: [7, 2] node: 516; worldview: 2; interests: [0] node: 531; worldview: 2; interests: [4] node: 546; worldview: 1; interests: [9, 7] node: 583; worldview: 0; interests: [3] node: 64; worldview: 1; interests: [2, 6] node: 663; worldview: 0; interests: [6, 0] node: 677; worldview: 2; interests: [0] node: 71; worldview: 2; interests: [2, 9] node: 723; worldview: 1; interests: [0] node: 765; worldview: 1; interests: [0] node: 807; worldview: 1; interests: [9, 2] node: 861; worldview: 2; interests: [5, 0] node: 862; worldview: 2; interests: [6] node: 9; worldview: 1; interests: [6] node: 901; worldview: 2; interests: [2] node: 930; worldview: 0; interests: [8] node: 954; worldview: 1; interests: [0]
And I can create subgraphs of the different worldviews in the ego network. This is the subgraph of worldview 1 nodes.
And since I have identified worldviews and interests, I can calculate modularity. This code is a bit gnarly, as I needed to just figure out an approach. Clean and good is later. But this works.
c1 = set(ego_df[ego_df['worldview']==0].index.values)
c2 = set(ego_df[ego_df['worldview']==1].index.values)
c3 = set(ego_df[ego_df['worldview']==2].index.values)
modularity = nx.community.modularity(ego, [c1, c2, c3])
In this ego network, there is a modularity score of 0.146. This was a lot of work to get to one number. There was a lot of setup involved. That is normal when trying to operationalize something theoretical. There is no cookbook for this, no one person for me to lean on. But what is this modularity score?
You can read more about it in the networkx documentation. The page also links to several other sources, including the book I mentioned in the beginning.
Basically, a positive score indicates assortative mixing (like attracts like) and a negative score would indicate the opposite (dislike attracts like).
I’m Still Learning
I am still learning. This is how I learn. I like to learn, and then show what I have learned. There is a saying that if you can’t explain something simply, then you do not understand it well enough. Storytelling is very good practice for communicating, but it also reinforces what we have learned.
This is a new concept for me, one that I haven’t explored or used in practice. That means I have a lot to think about, if I want to use this. I have to do certain things a little differently to even capture the context that is needed in this calculation. Community detection algorithms are not enough, as they just capture communities based on network placement and connectivity, not based on WHY the things are connected in the first place.
I’m not done with this simulation or this concept. Today, I wanted to get the simulation setup, even if not perfect yet. I have more to think about, more to experiment with. Now I can use this to get to know modularity better.
Code is Available
Today’s code is available. You can get it here. Keep in mind, this is very experimental. I encourage you to learn the concept and do your own experiment and simulation. Use mine for inspiration and take it further, or use it as inspiration and do something completely different. Play with simulation. Explore reality.
This is really fun programming. This is also a great way to learn to code, but significantly more challenging than the typical “build a calculator” or “write hello world” stuff.
That’s All for Today
Thanks to everyone who has been following along with this series. Happy learning! If you would like to learn more about networks and network analysis, please buy a copy of my book!